Posts

On a $1000 loan at 20% interest, why is my interest not $200 for one year?

/in , , , /by

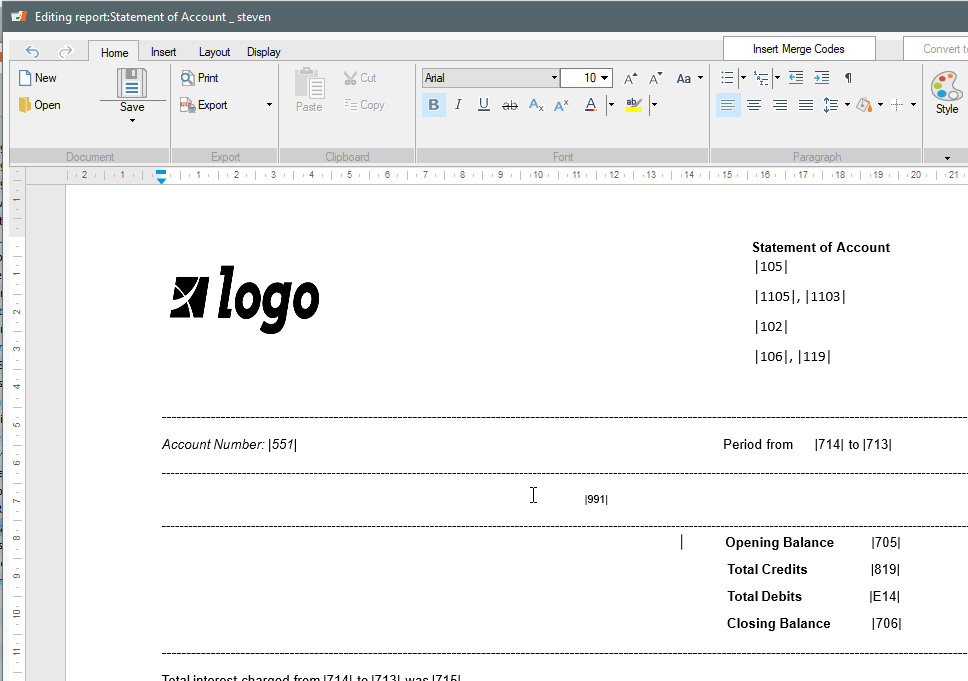
Q: On a $1000 loan at 20% interest, why is my interest not $200 for one year?

A: This is a common question that we often get and some information is missing to answer the question so we’ll analyse this, taking into account various scenarios and how to manage this in Margill Loan Manager.

There is a misunderstanding as to the concept of “amortization”.

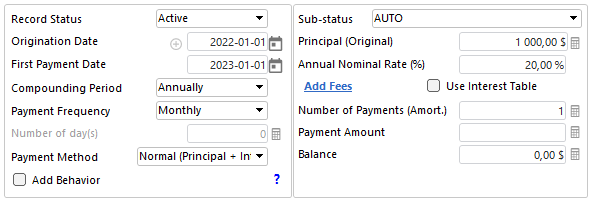
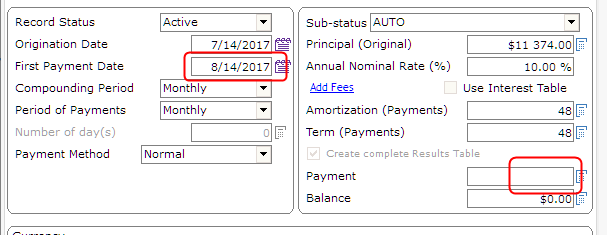
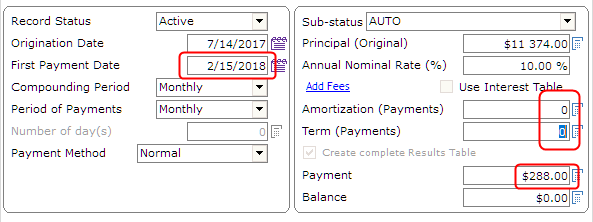
Here is how we get to $200 in interest on a loan. It must have ONE (1) lump sum payment at the end (one year later) of 1200 to get a balance of 0.00. So there is no amortization in this loan:

Compute to get the Results table:

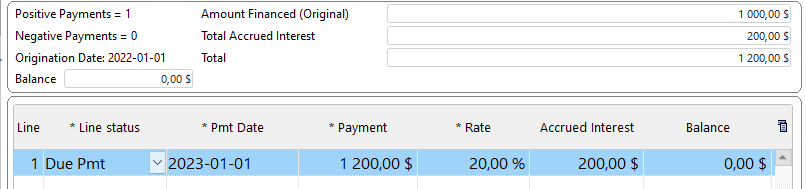
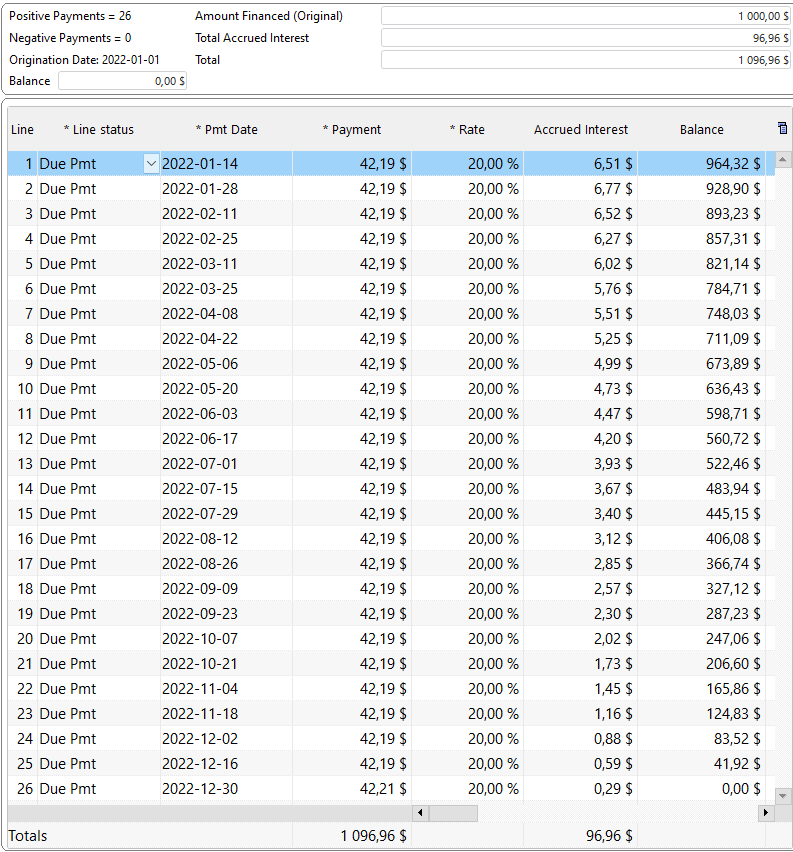
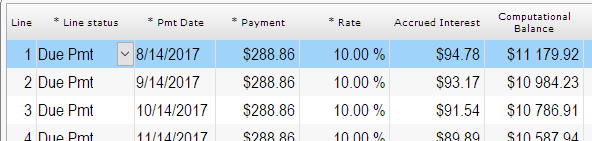
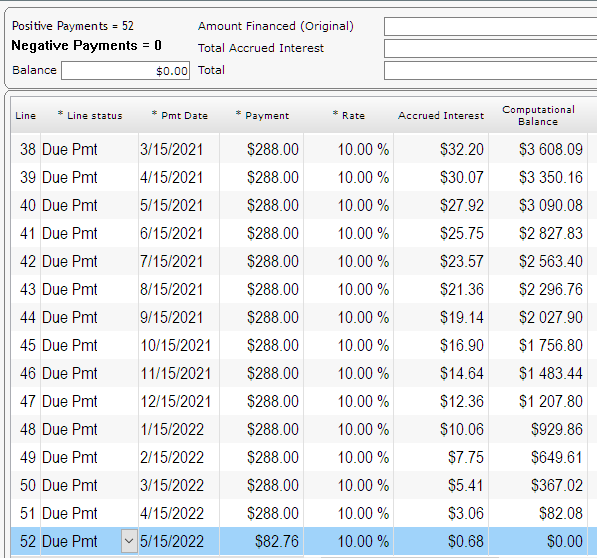
Let’s look at this with bi-weekly $0.00 payments just to see the interest accrued (so 26 payments and the last payment on Jan. 1, 2023 to give exactly one year). This is Compound interest (not Simple interest), so the interest keeps on increasing:

So you get exactly 200 (+ or – a few cents due to rounding) as the interest amount.
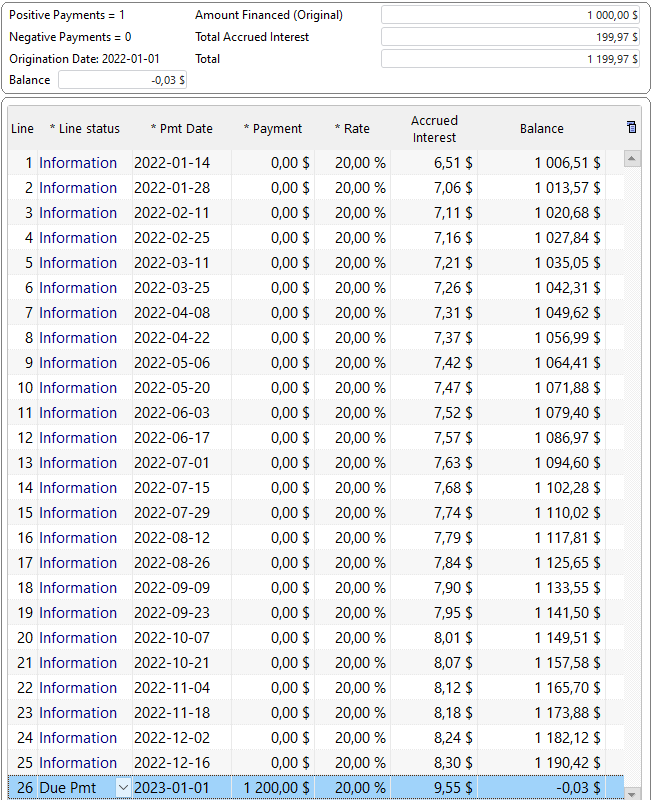
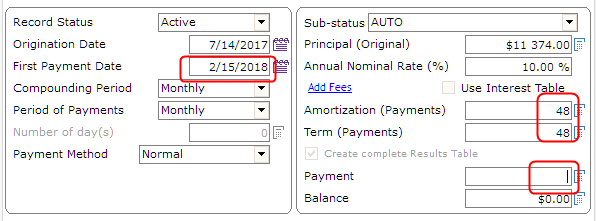
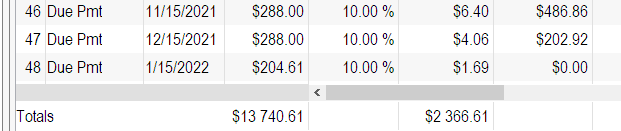
However, when you add true payments that pay interest and principal (every 2 weeks, so 26 for a full year approximately), you are not lending 1000 for 1 year since principal gets paid back every 2 weeks, thus reducing the interest accrued.

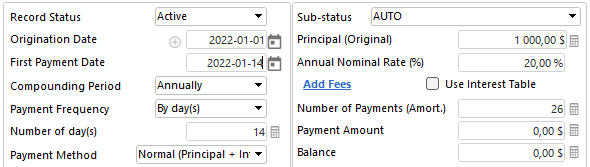
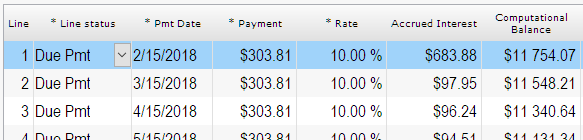
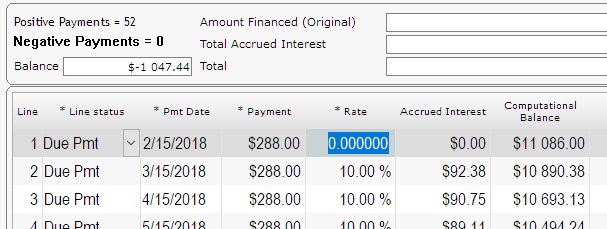
“Compute” to get a real amortization schedule at 20% annual (APR). Notice my balance goes down so the fortnightly interest (every 2 weeks) goes down and so does the interest per period. So for an amortized loan, the interest is very far from 200 total, only about half (96.96) because of the amortization effect.

There are two ways to get the desired $200 in accrued interest for 1 year when there are true principal and interest (P&I) payments:
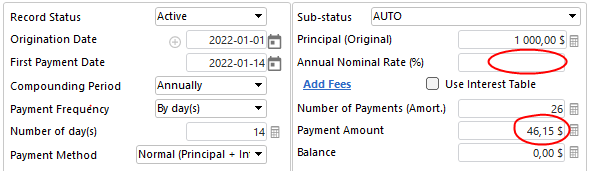
Method 1): Calculate the REAL interest rate
  • Desired Interest per payment: 200 / 26 = 7.69
  • Principal per payment: 1000 / 26 = 38.46
  • So 26 payments of 46.15 each (26 x 46.15 = 1199.90)
Leave the Annual Nominal Rate blank and enter the Payment of 46.15. Margill will compute the rate.

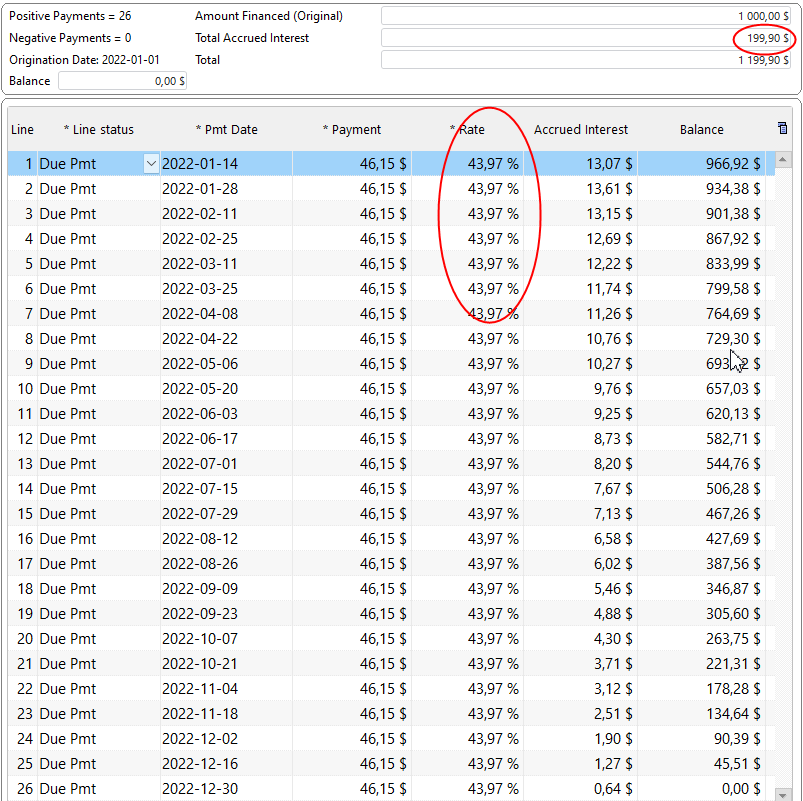
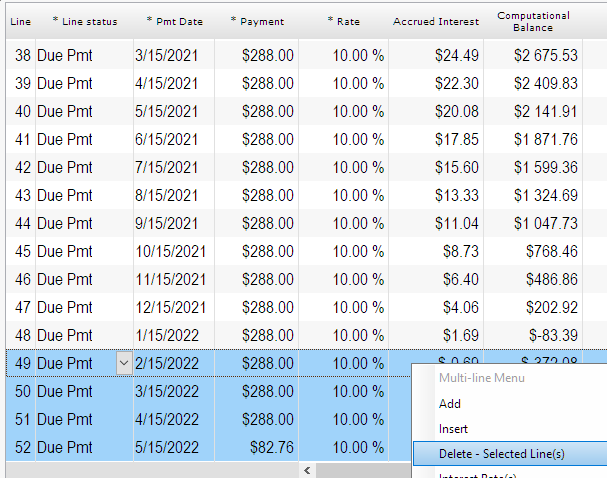
 “Compute” and notice the real interest rate (APR) is now 43.97% (APR). We are at 199.90 in interest (almost 200).

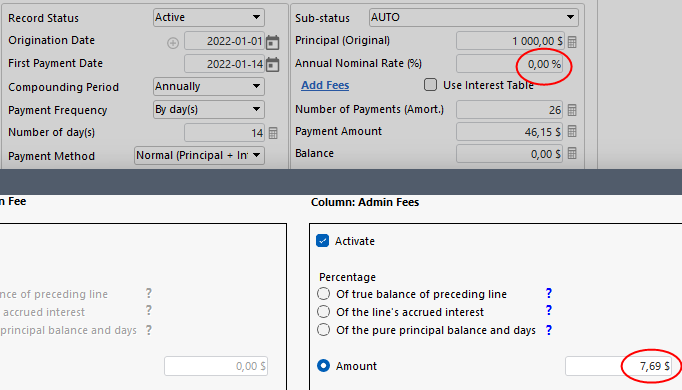
2) Use Fees, not true interest
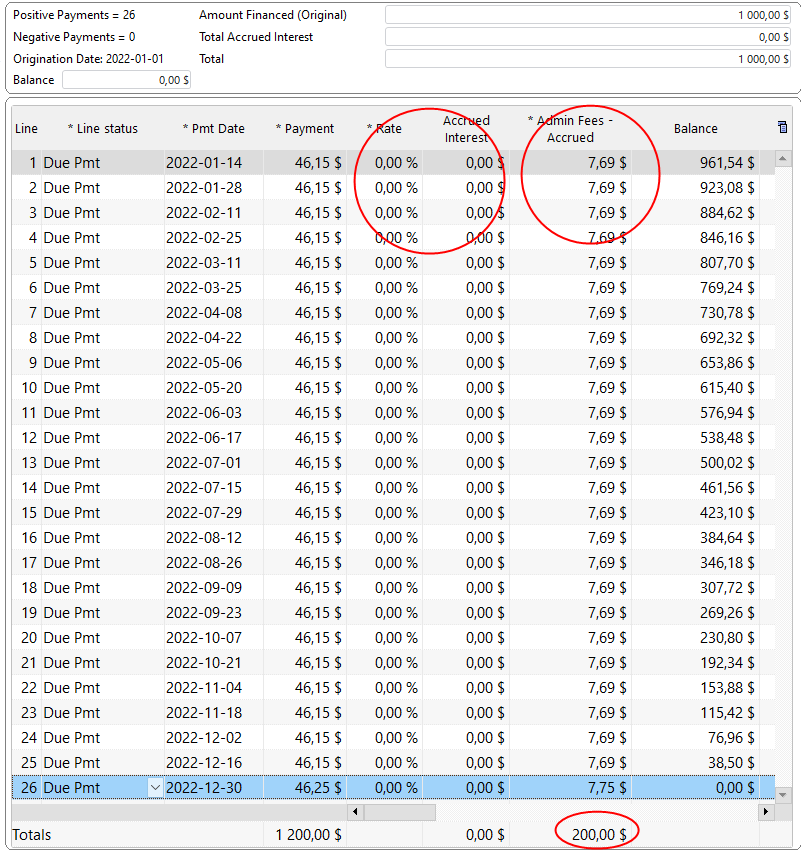
Other option is to use Column fees (that are not computed on a daily basis but entered once and no matter what, you will have 200 in “finance costs”, not real interest). Click on Add Fees (I called them Admin fees – you can rename them to anything you want) and add 7.69 (200 / 26) in “interest” (Admin Fees here) per payment.

Here are the results. I added a few cents in Admin Fees at the end and increased my payment to get exactly 200 as my finance cost. Notice my interest rate is 0% since I am now using Column fees, not real interest.

I also invite you to consult our White Paper on interest. It explains basics and more advanced issues with interest: https://www.margill.com/en/interest-calculation-white-paper/

Total Flexibility in your Payment Schedules

/in /by

Loan servicing made easy

Completely adapt a payment schedule to your borrower’s needs and real life such as irregular payments, seasonal cashflow, interest-only, principal-only, partial, late, unpaid payments, lump sum, automatic fees, negative balances in intercompany loans, interest rate changes, residual value…

 

Can we email an amortization report to each borrower when interest rates change?

/in /by

Margill Loan Manager – Can we email an amortization report to each borrower when interest rates change?

Yes this can be done.

First, I guess you updated the interest rates though the Main window with Ctrl Alt Shift i. Ideally you have a custom field that identifies the loans that are tied to the specific index (Prime, LIBOR, etc.). With this field you can easily select the proper loans to 1) change the interest rates quickly and 2) send the amortization schedule by email.

You could have the scroll menu with “Prime” or to be more precise “Prime +”

To create the statement to send out, go to Reports > Mail/Email Template > New and create a DocX that offers many more options than the older RTF.

You can then structure the template and enter your logo and add the Merge codes to identify the Borrower, etc. You could also create your statement in Word and copy it here afterwards.

Here is what this could look like (the |105| for example, are Merge fields)…

The merge codes to enter the amortization schedule per se are under the General theme. You can try each to see which is best for you. There are 10 templates and we can program others to meet you exact needs (columns included, titles, etc.).

 

Now that your template is created, test to see if all is good (numbers, names, etc.).

Go to Reports > Document Merge.

You will need to select a date range or show the entire schedule (past, present and future payments). I would opt for a date range to see up to the rate change, not the future.

See the circled red settings below. |991| will be the schedule…

Then press on “Save – Print -Send by Email”.

Here are the options:

You can also add an email  Subject and Message when sending the email.

Email sending must be configured in Tools > Settings > Email Connection. Your IT person will usually set this up properly for each Margill user.

The selected Records will all be sent out by email in a batch. Each takes about 10 seconds to create and send out.

Long first payment deferral versus normal one period (month) deferral

/in /by

Question:

When we compare a loan using a normal amortization schedule (amortization book or calculation on an online website) we do not reach the same number of payments in Margill as in the on-line calculator. Why is this?

Here is an example:

Origination Date:  July 14, 2017.
Original Principal: $ 11,374.
10% interest rate
48 months
Deferred interest and payments until Feb. 15 2018.

Normal amortization tables show payment of approx. $288.00 @ 48 months.
Margill is showing us 51 + payments @ $288.00.

Answer:

This is a most common error because of the “Deferred payment.”

Amortization tables (static) and on-line calculators cannot include deferred payments. They are usually exactly one period (often one month) after the Origination date. You could not thus get the proper payment with a 7 month deferral.

If I do a 48-month loan, with first payment exactly one month after July 14, I thus get the $288 you are looking for ($288.86 to be precise). Leave the payment blank so it is calculated.

So this is not what you are looking for since my first payment date is not properly deferred.

Let’s say we really do want 48 payments with the February date.

Because of the deferred first payment (6 months after a normal 1 month deferral) I am now at a payment of 303.81. Much higher since more interest accrued before any principal gets repaid.

From the screenshots you sent me, you want a 288.00 payment (not 288.86):

So I leave the the Amortization and Term blank and the number of payments will be computed to 52 with a last payment of $82.76.

 

Follow up question:

When I wrote “Deferred interest and payments” I meant thee is no interest from July 2017 to February 2018.

Follow-up answer:

You can simply change the Rate column to 0.00%. Balance then becomes minus $1047.44.

Then delete the extra lines (for which the balance is now negative) by highlighting them > right click with the mouse.

 We are now at 47 payments of $288.00 and the last one at $204.61 (since no interest for 7 months).