By: Marc Gelinas, Attorney, MBA
CEO, Jurismedia Inc. / MargillOriginally published in REAL ESTATE LAW & INDUSTRY REPORT (by The Bureau of National Affaires, Inc.)
Vol 1, No 4, Nov. 4, 2008, pp 119-122Last updated: April 2020
To read the original version, click here.
ABSTRACT: Over the last 30 years, computers have eliminated the need to understand basic interest principles. Consequently, many organizations, have forgotten many fundamentals, and the people who should know what standards and principles apply to their organization’s interest calculations instead rely on their computers and, very often, older software, which may be incapable of dealing with today’s complex market requirements.
The article deals with the fundamentals of applied interest calculation that include simple, compound, effective rate and add-on interest calculation methods, compounding period, repayment principles, day count (Actual/Actual, 30/360, Actual/365, Actual/360), annual percentage rate (APR) and more complex issues such as the number of weeks in a year, the weight of a month in a year and the non-negligible effect of leap year in high-stakes calculations.
More than Math
The Lost Art of Interest Calculation
Nothing seems simpler or less interesting than calculating interest. As well as your trusty calculator and spreadsheets (such as Excel), there are dozens of software packages that calculate interest on loans and mortgages. Yet, surprisingly, few of these packages provide truly precise results in situations that are irregular. People who compare their bank’s numbers with those derived via free or inexpensive software are always surprised to find that they are not the same. Why is this? Isn’t there a standard mathematical formula which everyone uses and provides the right numbers? The answer is quite simple: yes and no.
The heart of the problem is that, over the past decades, computers have eliminated the need to understand basic interest principles. Consequently, many organizations, large and small, have forgotten many fundamentals, and the people who should know what interest calculation standards and principles to apply, instead rely on their computers and, very often, older software, which may be incapable of dealing with today’s complex market requirements.
Laws such as the U.S. Truth in Lending Act, European Directives (Directive 87/102/CE (repealed), 2008/48/CE) and other national and regional (state and provincial) laws, regulations and “customs” provide some guidance for consumer loans, but they leave many blanks and many items to be dealt with in the loan agreement. Accordingly, this article is meant to give people who depend on interest for their livelihood (bankers, mortgage brokers and other lenders) and those to whom interest is important (real estate professionals, lawyers, accountants and other financial services providers) a comprehensive survey of the intricacies involved and the discrepancies that may occur in the calculation of interest. The text is thus divided into four sections: Basis Definitions, Basic Basics, Intermediate Basics and Advanced Basics.
Basic Definitions
A normal, basic loan consists of two components: principal and interest. Everything seems quite simple. However, the interest is dependent on a much more complex component: time. Time means days, months, years and it’s the time that determines the amount of interest which is the crux of the loan calculation issues. It is critical to understand these few fundamental definitions, more than otherwise, related to the time element.
Loan Amortization versus loan Term:
- Amortization: required period of time to settle (reduce) the principal of a loan in order to get a balance of 0.00 (or other residual value) at the end. The amortization period includes the payment of interest and principal.
- Term: period of time between the start of the loan and the end which is determined by the creditor and the borrower.
- Example: a mortgage can be amortized over 20 years (240 months) but have a term of 5 years (60 months), at which point the mortgage must be renegotiated.
Accrued interest, versus overdue interest, versus paid interest
- To an accountant, the difference between accrued and paid is obvious, but for non-accountants, the concept is often misunderstood. The difference between accrued interest and paid interest is particularly important depending on the creditor’s use of accrual or cash accounting.
- Accrued interest: interest due between the start (origination) date of the loan and the last date at which interest is due.
- Overdue interest: accrued interest which must be paid immediately, unconditionally.
Nominal interest rate / Effective interest rate
- Nominal interest rate: quoted interest rate for borrowed or invested principal. Does not take into account the compounding or capitalization of interest like the effective rate does.
- Effective interest rate: true percentage of interest that is paid or received on money borrowed or invested, as opposed to the nominal rate. The effective interest rate takes into account the interest compounding or capitalization. Please note that the effective interest rate does not take into account the fees charged to the borrower added to the original loan amount. APR (Annual Percentage Rate) includes interest and compulsory fees in order to obtain, the almost true cost of the loan.
Interest capitalization (compounding)
- When interest becomes due, it can be capitalized or added to the balance used to calculate the interest, thereby generating interest. Strictly speaking, unpaid interest that is capitalized is not added to the actual principal. Interest, even capitalized, does not become principal or capital. This interest is used to determine the “calculation balance” which is then used to calculate the next accrued interest amount. Interest is accounted for distinctly from pure accounting principal.
- Be wary in the above definition of the words “when interest becomes due”, since the compounding frequency in some interest calculation methods, that we will see below, have no connection with actual payment or not of the accrued interest. The compounding frequency is used to determine the “effective interest rate” and even in a loan in which interest is paid as scheduled, the total accrued interest will be higher when compounding is more frequent.
Finally, “principal” versus “principle”. Principal, also called “capital”, is the amount financed. Principle is the natural, moral legal rule or standard. Too often I have seen “principle” used to mean “principal” or “capital”.
Basic Basics
Simple or Compound interest?
The difference between simple and compound interest is quite straightforward: with simple interest, no interest is charged on interest. So, unless the principal decreases or increases, the interest calculated every day will remain the same. It is easy to understand that if this accrued interest is not paid by the borrower until much later, the creditor greatly loses.
With compound interest, accrued interest bears interest. Therefore, even if the borrower pays interest only much later on, the creditor will have benefited from additional interest on this interest and will not be penalized by the effect of inflation, which essentially reduces the value of his principal.
My fortune comes from a combination of living in America, some lucky genes and compound interest.
– Warren Buffet
Compound interest is a much fairer method for all parties involved even if we often see laws, regulations, case law and customs which state that simple interest must be used as a method unless the agreement or contract specifically states that compound interest was intended.
Simple interest is often used by creditors or investors with less experience since the calculation is simple and can be done easily. The formula for full periods:
Principal * interest rate for the period * number of periods = interest
Example: 10 000 * 1% per month * 6 months = 600.00
Of course, calculation becomes slightly more complex when the periods are not full, complete. We must then calculate by taking in account the number of days:
Principal * annual interest rate * number of days / days per year = interest
Example: 10 000 * 12% annual * 182 days / 365 days per year = 598.26
Notice there is a difference between the total interest between full periods versus the number of days. We must also see if it is a year of 365, 366, 365.25 or 360 days (see the Day count section).
Most normal, medium to long term loans from banks to consumers or businesses are calculated using compound interest. A sophisticated lender, such as a bank, understands that the risk in compound interest is less than with a simple interest loan since, if the borrower does not pay the interest, it will nevertheless generate additional income, provided of course that the debt does not become uncollectible.
For personal and commercial short-term loans, often offered by finance companies other than banks, simple interest tends to be the standard. Why? In my opinion, because the calculation is really easy: by calculating the number of periods (3-month loan, 2% per month and there you have it! Interest is the same for each of the three months). These companies quickly realize the flaw in using this simplified method when the loan is paid in advance or late in which case they must change their calculation method to exact days. Even longer-term loans from lenders other than banks are often calculated with simple interest, but this should not be the norm.
Simple interest is found in the legal arena, as when interest is payable in civil liability matters, but the courts are increasingly considering compound interest, which more accurately reflects “real life”. In the United States, federal government agencies charge compound interest not simple interest (they use Capitalized simple interest – see further in the article).
Effective Rate method vs. Capitalized simple interest
Compound interest may be computed in different ways. The most common confusion stems from the “Effective” rate method (some may call it “Actuarial method” but there is controversy at this level since country legislations will use different terms) and “Capitalized simple interest”. Generally, these two methods will give equal results for regular loans (regular payments on regular payment dates that are respected) but any irregular event (payment ahead of time or late payment for example) will generate a slightly different interest total depending on the method used. Even if the differences are small, a conflict could arise between the creditor and the borrower over who is right. We have seen situations where creditor and debtor did not agree with the other’s balance and in the end, neither of them wanting to change their method for a few dollars, the only winners were the lawyers!
Capitalized simple interest is an easy method of computing interest (often used in spreadsheets or with pocket calculators) but is not always fair for the lender and borrower. With this method, the same amount of interest is computed daily throughout the period and at the point of capitalization (compounding) the total interest generated is added to the balance. This balance becomes the new principal upon which interest is computed until the next capitalization. This method is actually simple interest divided with capitalization of interest at regular or irregular intervals.
Here is an example with monthly capitalization:
Month 1 : 10 000.00 * 1% monthly * 1 month = 100.00
Month 2 : 10 100,00 * 1% * 1 = 101.00
Month 3 : 10 201,00 * 1% * 1 = 102.01
Month 4 : 10 303,01 * 1% * 1 = 103.03
Month 5 : 10 406,04 * 1% * 1 = 104.05
Month 6 : 10 510,10 * 1% * 1 = 105.10
Total : 615.19
If interest was to be paid at each capitalization’s “anniversary”, then we would have simple interest. The capitalization factor disappears.
The Effective rate method of calculating interest computes interest in one operation based on a slightly exponential formula that uses the nominal interest rate that has become an effective interest rate because of compounding. The interest generated on a daily basis at the start of a period is less than that earned daily later on in the loan. Daily interest thus changes from day to day.
Basic formula for full periods:
Interest = Principal (1 + i/n) EXP (n*t) – Principal
i = annual nominal interest rate
n = compounding period frequency
t = time in number of periods of loan
Our example:
Interest = 10000 (1 – 0,12/12) EXP (0.5 * 12) – 10000
Interest = 615.20
Notice that the amount of interest calculated with the Effective rate method yields the same result as that with Capitalized simple interest because the calculation is perfectly regular and for full periods. Both methods would not yield the same results in irregular scenarios.
While remaining unchanged at the mathematical level, the formula for the effective rate becomes much more complex for fractions of periods, to take account these irregular periods. More sophisticated software is thus required which takes into account fractions of periods.
For loans calculated using the Capitalized simple interest method, the borrower pays more interest in the first few months than what would have been paid using the Effective rate method. The Effective rate method treats both the borrower and the creditor fairly, and an increasing number of jurisdictions have, and require, consumer loans to use this.
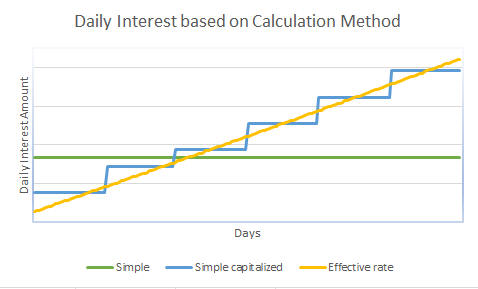
Period of capitalization / compounding
When talking about compounded or capitalized interest, one must specify the compounding frequency (annually, monthly, daily, etc.). The frequency varies depending on the type of loan, certain laws and industry practices. The interest rate charged (or effective rate) is higher when the compounding period is daily and it diminishes as the period gets longer: weekly, every two weeks, monthly (most mortgages in most countries), quarterly, semi-annually (mortgages in Canada) and annually.
In a contract, the “nominal” interest rate is usually written along with the compounding frequency which determines the effective rate (or real rate).
| Nominal rate: | 12 % | 30 % |
| Effective rate | ||
| Annually | 12.0000 % | 30.0000 % |
| Semi-annually | 12.3600 % | 32.2500 % |
| Monthly | 12.6825 % | 34.4889 % |
| Daily | 12.7475 % | 34.9692 % |
Disclosing the effective rate would, of course, give a more precise idea of the real cost of the loan to consumers (we will discuss the “really real” interest rate later, also known as Annual Percentage Yield (APY) which takes into account the fees charged in the loan and the compounding.
What about Add-on interest? Low rate mirage….
Also called “pre-calculated” or “pre-computed” interest or the “flat-rate method”, the total interest, calculated as explained below, is “added on” to the original principal and the result is simply divided by the number of payments to be made. This makes for simple calculations and is often used in vehicle finance and in other micro loan programs. However, the buyer isn’t always aware that the interest charged is almost double the stated rate.
Add-on interest works like this. A rate of $12.50 per hundred per year (or 12.5%) charged on a $20,000 loan to be repaid in monthly payments over 4 years will give us a total add-on charge of $10,000 (20,000/100 X 12.50 X 4). The total loan is thus $30,000 to be repaid in 48 equal payments of $625.00.
Many have difficulty understanding that the rate that seems very reasonable when disclosed as an add-on interest amount or rate, is in fact very far from the APR that must be stated for disclosure, since add-on interest does not factor in principal amortization for each payment. APR disclosure and laws that fix the maximum interest rate that can legally be charged to consumers, require that the rates computed be mathematically sound.
Except in certain scenarios (interest-only payments and when payments are insufficient to even pay off the interest portion), when a payment is made, principal and interest are usually paid back to the creditor by the borrower. Nevertheless, with add-on interest, the 12.50% is always charged on the original principal, no matter what principal is paid back to the creditor. After 6 months, if $1500 in principal had been paid back to the creditor, he could lend out this amount and profit from it once again while the add-on interest borrower continues to pay interest on the full initial amount.
Another problem occurs when the borrower misses a payment. Would interest be charged on this amount? If so, then double interest would actually be charged.
The effective rate of our 12.5% add-on interest is actually over 21.5%.
Rule of 72, Rule of 78
Since these rules were created before the advent of the computer and are now outdated, the article will not deal with these “shortcut” methods. These calculation methods should no longer be used. They have been developed simply to estimate but cannot be used to obtain precise data.
Start date, Maturity date
In a loan, it may sometimes be difficult to decide whether to include the final (or maturity) day in the interest calculation. Generally, subject to a few exceptions in certain countries, the maturity day is not counted when calculating the days of a loan – only the elapsed number of days is counted. The logic is quite simple, as illustrated by this example. How much interest is payable on a loan of $10,000 for one day? With a start date of April 1, say, should the end date be April 1 or April 2? The latter is more logical, since it takes into account all of April 1 to midnight minus one second (let’s say less than a fraction of second), and only one day’s interest is payable.
We have also seen the opposite scenario where accrued interest from the origination date must be excluded from the calculation but that at the end date must be included. In my opinion, this method is less common and should not be used. It can stem from an agreement between parties who decided so, and we could argue that the loan is made at the end of the day and paid at the beginning of the day to justify this method, but it is not the norm.
This date inclusion and exclusion sometimes leads to important errors in spreadsheets because the last day of interest of the year is often forgotten (generally December 31) when running reports. Often, the report is run improperly or the data simply not available in spreadsheets since the calculation is made on the morning of December 31 (0:00) as opposed to midnight (or 0:00 on January 1st). Millions of dollars are lost (and gained by the other party) each year because of this problem. It is therefore important to verify that the last day of the year or the month is properly accounted for (and billed to the borrower) in the calculations.
See: Loan Servicing with Excel? Pitfalls and alternatives
Intermediate Basics
Day count
The Day count is the method by which the number of days between two dates (loan date, payment (coupon) dates, end date) is counted. Even if practice does not reflect theory, all loans, mortgages and bonds must specify which Day count is to be used for interest calculation. It seems simple but there are no less than 20 Day count methods, depending on country, industry, client type and type of financial instrument!
The four most common Day count methods are outlined below. Depending on country and industry, there may be variants in the names used. These names follow the ISO 15022 nomenclature:
- Actual/Actual, sometimes known as Actual/365 (ISDA), is the most intuitive and precise Day count scheme. To determine the number of days between any two dates, the actual number of days, including the effect of a leap year, are counted. This method is used for treasury bonds and notes, and unless otherwise indicated by law, contract or “custom,” it should be used for maximum precision, although it can be relatively difficult to apply in spreadsheets as we will see in the “Advanced Basics” section.
- The 30/360 method, also known as “Bond basis,” was invented in the days before computers to make computations easier. In this method, all months, including February, have 30 days, and all years have 360 days. In the U.S., 30/360 is used for corporate bonds, U.S. agency bonds and mortgage-backed securities. Without a sophisticated calculation software, this method becomes complex to manage for irregular loans as reflected in this example: the number of days in a leap year, between February 1, and February 28 (at 12:00 AM) is 27 while the number of days from February 1 to February 29 (at 12:00 AM) is 29 days, two days more for the additional day. Various sub-methods, including the 30/360 U method, have been developed to count days differently, especially for the month of February.
- The Actual/365 (Fixed) method counts the actual number of days of a loan, but the denominator (used to calculate a daily interest rate) will exclude the extra day in a leap year. Thus, a daily interest rate, is always the yearly rate divided by 365 (for calculations using simple interest).
- Actual/360 is a slightly odd method, which counts the actual number of days during which a loan is outstanding and calculates the interest rate based on a 360-day year. So, over one year, a $1,000 loan at 10% will yield $101.39 in interest (365/360) as opposed to the annual return you would have expected of exactly $100. This type of count obviously benefits the lender. We see this method especially in the United States and on the money market in the Euro zone.
Annual Percentage Rate (APR) and Annual Percentage Yield (APY)
The APR is a “standardized” rate (expressed as a percentage), which takes into account all compulsory finance charges (interest and fees) associated with a loan. It is commonly used to compare loan programs offered by different lenders. The US Truth in Lending Act and laws in most western countries require consumer loan and mortgage companies to disclose the APR when they advertise a rate.
The APR expresses the real cost of borrowing. It also considers when fees are paid: financing fees, including interest and other mandatory fees that must be paid by the borrower over the term of the loan. Fees paid at the beginning of a loan will have a different effect on the APR than those paid at the end or paid monthly. Some fees are financed in the loan and will generate additional interest. This also has to be taken into consideration, when calculating the APR. If lump sums are paid, they will also affect the APR, as they lower the interest charges.
There are many interest-calculation software packages out there, lots of interest-calculation methods for amortization and, unfortunately, various APR formulae. The differences in the results obtained via these methods are usually quite small and, one hopes, within the acceptable 1/8% to 1/4% (irregular transactions) accuracy usually required by law.
In some countries, such as France, the law stipulates tough sanctions on inaccurate APR disclosure: the interest on consumer loans being reduced to 0% and the application of a very low statutory interest rate on commercial loans. Conclusion: don’t mess up the APR calculation!
Unfortunately, there are also many types of APR: actuarial, US Rule, nominal, effective, real and historical. Thus, it’s not always easy to navigate these waters. In the US, there has been some effort to standardize APR, but resistance is strong, because changing something that is already confusing may confuse consumers even more. APR only takes into account the nominal interest (and not the effective rate) and mandatory fees. In Europe, tougher standards have been applied where a true APR must be used: the “effective APR” that takes into account all mandatory fees as well as the compounding period. The effective APR is in fact known as Annual Percentage Yield or APY, the TRUE interest rate that takes into account fees and compounding.
Repayment order of loan components: Principal, Interest and Fees
Whether you are using simple or compound interest, accrued interest is usually paid before the principal. It is only when the payment is higher than the total accrued interest would the principal balance be reduced. This is called interest not paid in advance as opposed to the less common method where interest is calculated and paid in advance (other term: discount loan).
Of course, the most common way to pay accrued interest before principal is not always respected and we often see situations in which the principal is paid before the outstanding and accrued interest. In simple interest, this offers an important advantage to the borrower since outstanding interest does not bear interest. In compound interest (effective rate method), interest is charged on interest and so whether principal is paid first or not, the effect will be from an accounting perspective, not a mathematical one.
Finally, when fees are charged in addition to interest, these are generally paid or reimbursed to the creditor before interest and principal. This is not universal and again, some jurisdictions, especially in legal matters, will require that the principal be paid before interest or fees. So there are no real standards in this regard.
Advanced Basics
This section concerns subtleties that may produce minor differences in interest totals, often within the allowable margin of error. Far too often, the cause of such discrepancies is that the calculation software being used is incapable of handling these subtleties.
Calculating periods in a year
The math behind interest calculation and amortization schedules requires that the number of periods in a year be known. This may seem quite straightforward, but there are a few areas of confusion.
– Number of weeks in a year
In calculating the amortization when the payment or the compounding period is weekly, biweekly or every four weeks, different software packages will use different numbers of periods per year.
For example, in a 365-day year, weekly payments or compounding may occur 52 times per year or 52.143 times (365/7) or even 52.286 (366/7) times.
Although there are few norms and the differences between the results are quite small, software should include these options.
– Relative weight of months
Logic tells us that one month is 1/12 (0.0833) of a year and the interest for a full month should be this fraction.
Another possibility is to base the interest on the number of days in each month. By this method, January would count for slightly more than one-twelfth: 31/365 (0.0849) — or 31/366 (0.0847) in a leap year, if the Day count is Actual/Actual). So, what about February? Should less interest be paid in February than in a 31-day month? Using this method, yes.
Generally, in regular calculations with regular payments, the first method is more widely used, but both methods are acceptable.
Denominator year basis
When using the Actual/Actual method of simple interest calculation to determine the interest on a loan or a period of a loan (formula: principal balance * yearly interest rate * number of days/number of days in a year), leap year has a subtle effect on the “number of days” (the denominator). Various methods are used to determine whether it will be 365 or 366 days.
One method divides the calculation to take into account, as a reference, the civil year. The example in Table One illustrates the calculation method by which the interest accumulated from Nov. 1, 2019, to Dec. 1, 2019, is principal (or balance) * yearly interest rate * 30/365. In the bond market, this is called the ISDA method (International Swaps and Derivatives Association).
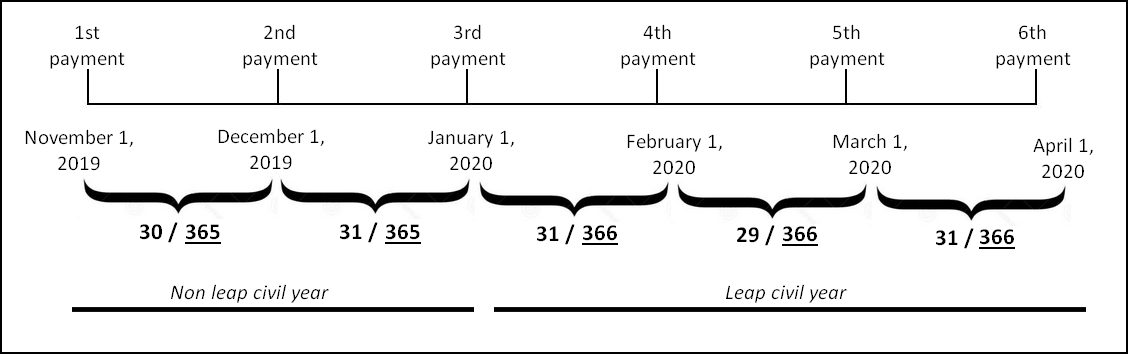
Tableau One: Civil year method (ISDA)
A second method, slightly more complicated, takes into account the payment anniversary date to calculate the base year. The example in Table Two shows the calculation method by which, counting backwards, the number of days is taken from the end of the actual payment period to a year prior. For the interest accumulated from Nov. 1, 2019, to Dec. 1, 2019, this method will take into account the anniversary date (December 2019 back to December 2018), to calculate the number of days in that year. Since there are 365 days in this period, 365 will be used as the base. For the March 1, 2020, to April 1, 2020, period, the 366-day basis will also be used, because from April 1, 2020 to April 1, 2019 (counting backwards), there are 366 days.
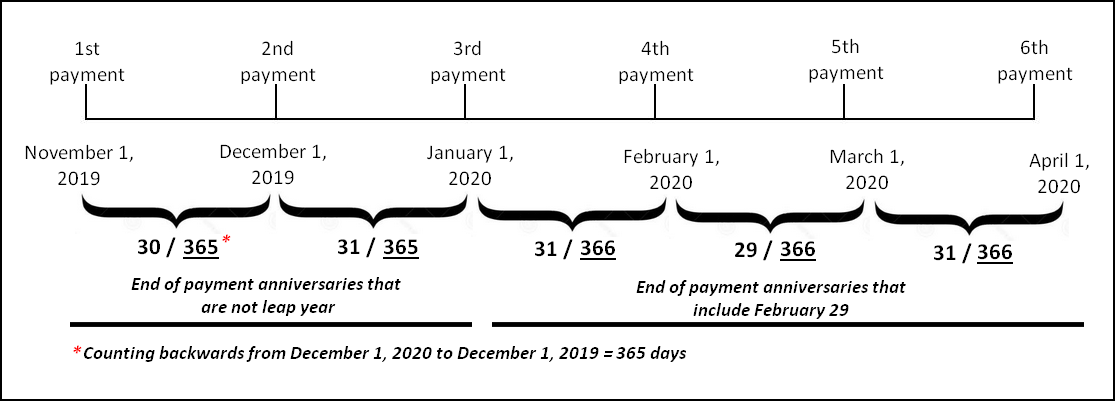
Table Two: Anniversary method
In the bond market, other methods include ISMA (International Securities Markets Association) and the AFB (Association Française de Banques), which borrow aspects of the above methods but with certain subtleties that will not be looked at here.
“Short” and “Long” periods in Compound interest
Finally, an oddity, which probably reflects a lack of proper calculation tools in the distant past. In some jurisdictions, when a payment on a regular compound interest (effective rate) loan is late or otherwise irregular, the simple interest method is used to calculate the interest for the period. We often see this in mortgages when the first payment date is not exactly one period after the origination date (usually monthly payments). For example, a loan is made on March 12 and the first payment by the borrower must be made on April 1st. The period between these two dates is considered to be “short” and interest will be calculated in simple interest for those 20 days (March 12 at 0:00 AM to March 31st at midnight). On the other hand, for a loan starting on March 12 with the first payment (principal and interest) on May 1st, this period will be considered “long” or even made up of a short period and a normal period. Some creditors will add a payment on April 1st to only cover the interest. Calculation of interest for 20 days will be made in simple interest. This additional payment is called the “Adjustment date” for interest and consequently allows this payment to be ignored in order to generate a regular and standard schedule that can be calculated with less sophisticated applications or even with paper amortization tables (these old booklets which included multiple amounts borrowed, rates and years of amortization in order to find the monthly payment!).
Another situation where we see this happen is, if a payment due on the 1st of a month is not paid until the 12th, interest would be calculated in simple interest this way: (balance * daily rate * 12/31) + (balance * daily rate * 19/31) for this period only. Although it is historically understandable and the difference between the two methods is quite small, we find this sudden change of method awkward and difficult to justify in the computer age. The effective rate method, on the other hand, would continue to calculate interest normally for this period, with the prescribed formula (exponential formula detailed in a section above) while calculating the days accrued and creating reference periods in order to complete the variable “t” (time in number of periods of the loan) of the formula.
Conclusion
This survey has highlighted the sources of the widespread confusion I have observed over many years of studying applied interest principles, working with clients and seeing what the market has to offer in terms of solutions. It is hoped that, when the numbers just don’t add up, these basics will steer the professional dealing with interest toward accurate and satisfying solutions.
When legislation does not specifically provide a solution, one should be aware of the possibilities and where discrepancies may lie. Moreover, to ensure maximum precision in interest calculations, the elements outlined above should be included in the calculation parameters detailed in the loan agreement, as is done in major international transactions.
Bibliography:
- Broverman, Samuel A, Mathematics of Investment and Credit, Second Edition, Actex Publications, 1996
- Chouinard, Pierre, Mathematics of Interest, 1990
- Code de commerce, France
- Cost of Borrowing (Banks) Regulations, Justice Canada, DORS/2001-101
- Directive 98/7/EEC, European Community
- Directive 87/102/EEC, European Community
- Kellison, Stephen G, The Theory of Interest, Irwin McGraw-Hill, 1991
- International Swaps and Derivatives Association web site: isda.org
- Late Payment of Commercial Debts (Interest Act), United Kingdom
- Margill, interest calculation, User’s Guide and web site margill.com
- Mayle, Jan, Standard Securities Calculation Methods, Volume 1, Third Edition, Securities Industry Association, 1996
- Ménard, Louise, Dictionnaire de la comptabilité et de la gestion financière, Third Edition
- SWX Swiss Exchange, Accrued Interest & Yield Calculations and Determination of Holiday Calendars
- Truth in Lending Act, Regulation Z, U.S. Federal Reserve Board
About the author
Marc Gelinas, Attorney, MBA (McGill University, Class of 1994), is the founder and CEO of Jurismedia, Inc., which develops Margill software products, interest-calculation and loan servicing software solutions used by thousands of lenders, accountants, bankers, mortgage brokers, lease professionals, attorneys, judges, trade unions and financial planners in over 40 countries. As a lawyer, he has, over the last 25 years, been called upon to resolve many complex issues dealing with interest and its accuracy in the U.S., Canada and Europe.
Email: [email protected]
__________________________________
To read the original version of the White Paper, follow this link.
