Loans
See also:
The dollar ($) has been used in these examples, but any other currency (€, £, F, ¥, R, DA, Rs… etc.) may be used.
Most of the calculations below may use Fixed (unique interest rates) or Variable rates.
Real-life examples:
Simple loan between two dates (simple interest)
Simple loan between two dates (compound interest)
Irregular loan : refund interest only, then of a fixed principal amount and a regular refund. Let’s include missed and late payments and even a NSF check!
Loan that includes successive disbursements and reimbursements
Loan that includes unknown future interest rates with payments adjusted as these rates become known
Add-on interest loan (often used for car loans)
APR (Annual Percentage Rate) calculation
Simple loan between two dates (simple interest)
Input screen:
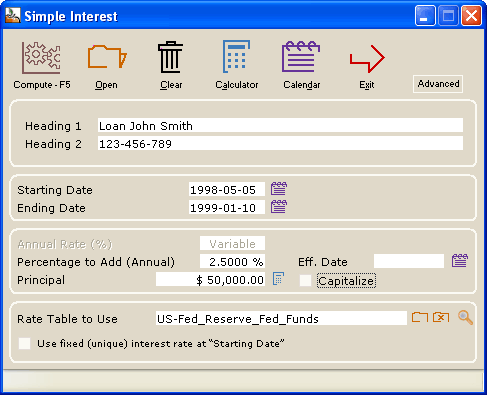
- This example uses the most precise calculation method (Actual/Actual or Actual/365) but other day count conventions may be used : 30/360, Actual/360 and Actual/365(Fixed).
- Interest (x%) may be added or subtracted to the variable interest rates indicated in the interest table created –Percentage to Add (Annual).
- This added (or subtracted) interest rate can take effect at any time during the calculation – Eff. Date.
- The simple interest may be capitalized (compounded) at the anniversary date – __ Capitalize.
- Choose
 any interest rate table among the many interest tables (Central bank rates for example) or create your very own.
any interest rate table among the many interest tables (Central bank rates for example) or create your very own. - You can see the interest table dates and rates by pressing on the
 .
.
Results screen:
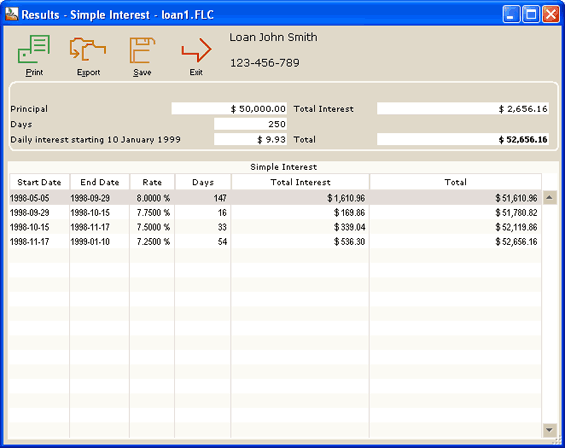
- You can divide the Total Interest in a fixed rate portion and a variable rate (not shown in example).
- Results can be exported to TXT format (Export button) or Word, Excel, XML (Web) (right click of the mouse).
- Results may be printed in a concise report.
Simple loan between two dates (compound interest)
Same features as simple interest but you can use compound interest with the following compounding periods : annually, semiannually, quarterly, monthly, every 4 weeks, twice monthly, biweekly (every 2 weeks), weekly, daily.
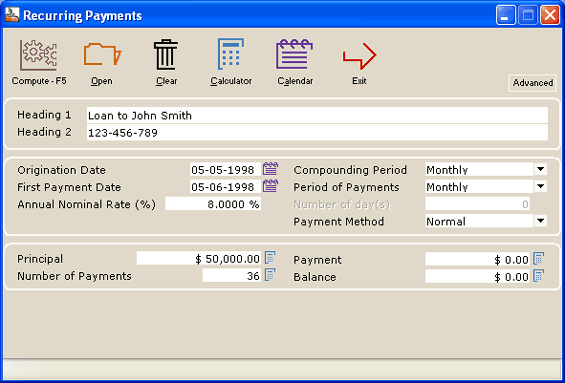
Loan with regular payments (refunds)
This example uses the 30/360 day count convention but other day count conventions may be used Actual/Actual (most precise), Actual/360 and Actual/365(Fixed).
Enter 3 of 4 variables (Interest, Principal, Number of payments or Payment) and the 4th will be calculated automatically.
Once a preliminary schedule is created, this may be totally changed to enter lump sum payments, extra payments, changing payments, new principal, etc. See the example in the next section.
APR can also be determined…
Irregular (complex) loan
This example uses the most precise calculation method (Actual/Actual or Actual/365) but other day count conventions may be used : 30/360, Actual/360 and Actual/365(Fixed).
The calculation will include the following : Refund interest only, then of a fixed principal amount and a regular refund. We’ll then include missed and late payments and even a non sufficient funds (NSF) check!
Input screen:
We first reimburse the interest only and produce our payment schedule.
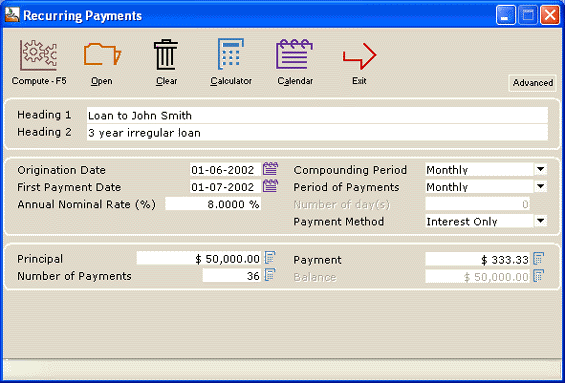
Here is the initial payment schedule:
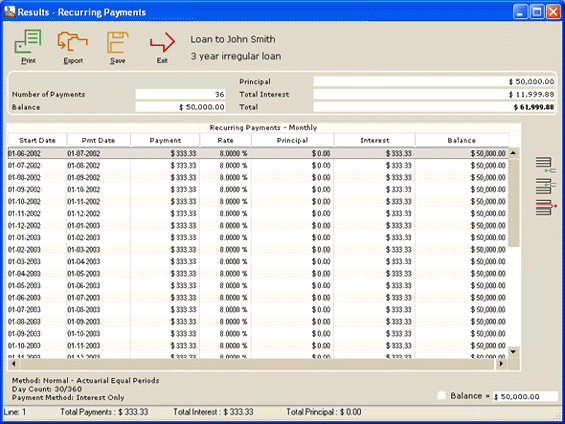
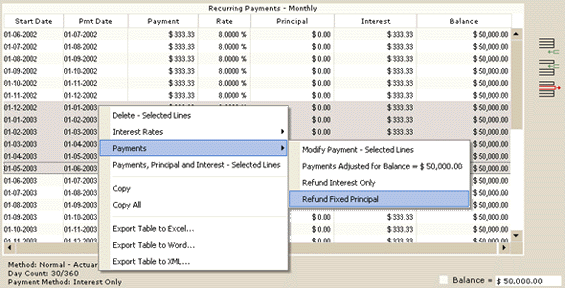
We want to refund Interest only for 6 months and then refund a Fixed principal amount of $1000 per month for 6 months. We simply select those lines (payments) we wish to change. Margill recalculates afterwards.
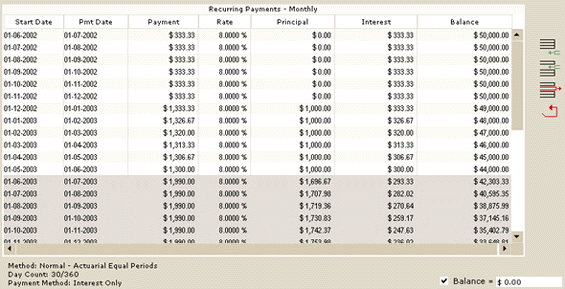
For the two last years we refund normally (principal and interest) to provide a balance = 0.00. Margill calculates the payment automatically. In this example (see below), with a payment of $1990.00 for the 2 remaining years we finally reach a balance = 0.
Unfortunately, our debtor does not follow the payment schedule and make a few irregular payments:
- The May 1st payment is only made on May 10th.
- The July 1st payment is missed altogether.
- The October 1st payment is an NSF with $25 fees charged by the lender.
- The debtor then tries to make up by making an extra payment of $2500 on December 15. Insert a line by clicking on the
 icon.
icon. - Starting January 1st, 2005, the interest rate changes to 9.5%.
The balance is recalculated automatically. The final yearly payments could also have been recalculated to give a $0.00 balance.
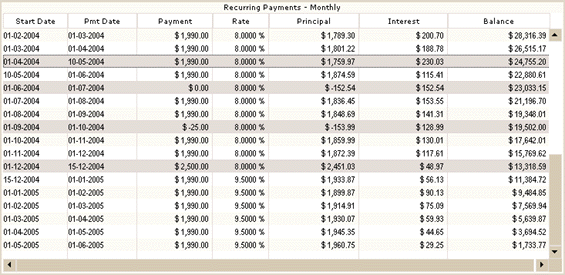
The payment schedule may then be saved and updated as time goes on.
Loan that includes successive disbursements and reimbursements
Example coming soon.
Loan that includes unknown future interest rates with payments adjusted as these rates become known
4-year loan based on Bank XYZ’s prime lending rate + 3%. In June 2005, the rate is known for the next 6 months and is at 4.25% + 3% (for the sakes of this example, the compounding is daily). The next rate will only be known in 6 months.
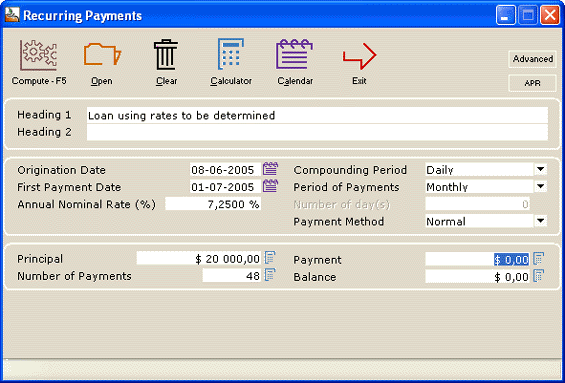
A preliminary schedule is first created with the known interest rate of 7.25% and as the new rates are known, the payment table will be updated.
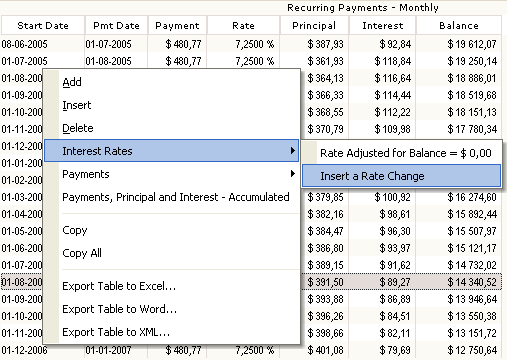
On December 15, 2005, the new rate to apply is 8.75%. The following window allow to insert the new rate and, if required to recalculate the equal amount payments to give a balance = 0.00 (or other amount. Margill will recalculate the payments.
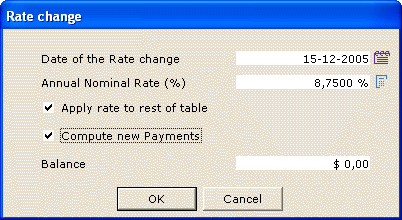
The new payments are thus increased since the interest rate increases. The table may se saved and updated as new rates are known.
Add-on interest loan
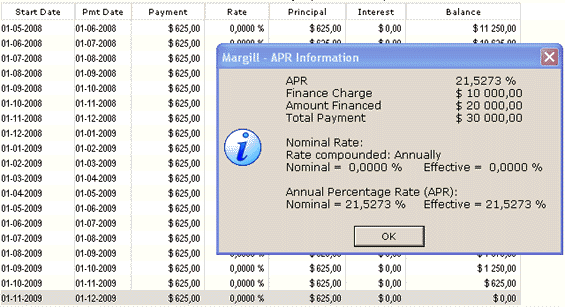
Add-on interest is a peculiar calculation which Margill can do easily and compute its true interest rate (APR).
For example, a car seller advertises a rate of $12.50 per hundred per year on a $20,000 loan to be repaid in monthly payments over 4 years.
How much interest is payable? What is the interest rate (or APR) on this loan?
This will give us a total add-on of $10,000 in interest: 20,000/100 X 12.50 X 4. This $10,000 is added in the APR screen within the Recurring Payments (Amortization) calculation.

The total loan is thus $30,000 to be repaid in 48 equal payments at “0.00%” interest. The compounding period is not important since for the reimbursement, the interest rate is 0.00%.
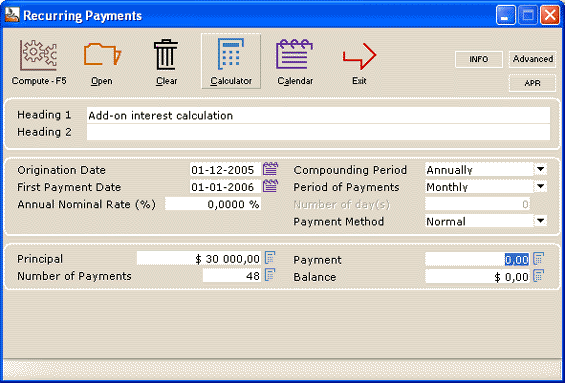
The payment will be calculated by Margill ($625 per month) and the effective rate determined to be 21.5273% (thus the APR).
Line of credit
A line of credit can easily be calculated with Margill.
- On May 16, the line of credit is activated with a withdrawal on the same day of $1500. This will be our starting principal (amount owed to the bank).
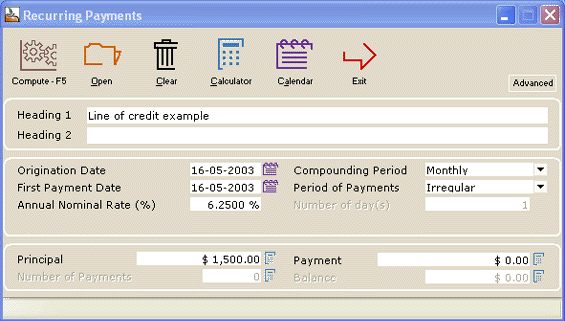
- A second withdrawal of $2500 is made on June 1st (insert a line
 with a negative amount for a withdrawal – new principal)
with a negative amount for a withdrawal – new principal) - A third withdrawal of $1750 is made on June 16
- The borrower then refunds $2000 on July 3 (a refund is a positive amount reducing the principal)
- and so on…
The schedule may then be saved and updated as time goes on.
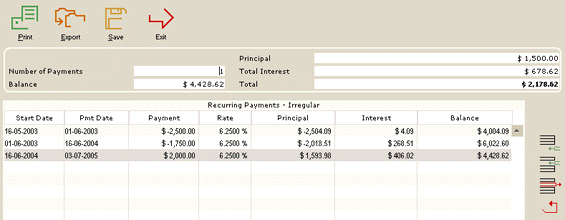
Compound interest is charged in between each of the payments/refunds. The interest is automatically calculated every day (as provided by the normal actuarial method) even if the compounding period is not daily.
Calculation of the unknown interest rate applicable to a loan with irregular refunds (determination of the contractual rate)
A loan is made with regular or irregular payments but with an unknown interest rate. Margill can easily determine the rate applicable to this loan.
In the Fixed Rate Calculations, Recurring Payments date entry screen, simply leave the rate at 0.00%. The prompt will appear
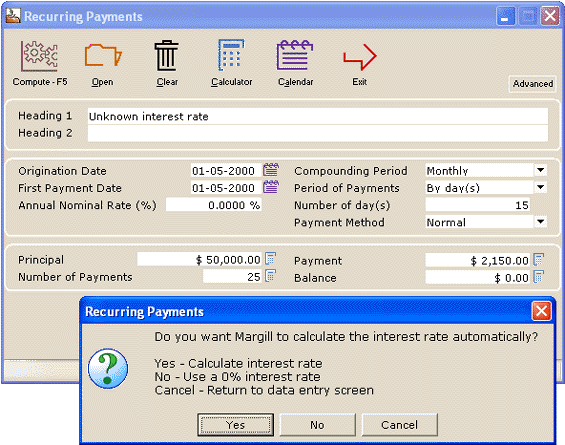
The rate will then be calculated and the Results screen will appear:
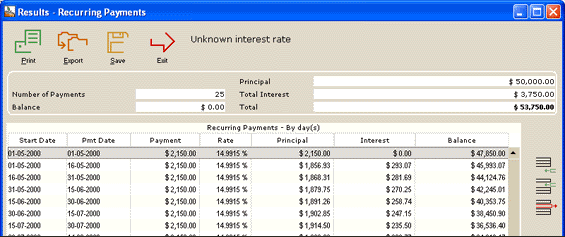
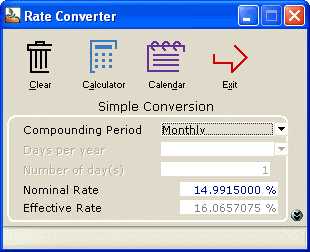
Our nominal interest rate is 14.9915% compounded monthly. We can use the Rate converter to obtain the effective interest rate:
Now for a more complex example where the payments are irregular. We will use our previous example, customize the schedule with irregular payments and calculate the new interest that yield a balance = $0,00 or any other amount.
In this example, we increased or reduced payments, added new payments and even added a new loan (the minus $4000). All these changes are all highlighted here in gray… The new nominal interest rate is thus 33.2782% compounded monthly to reach a balance = $0.00. The balance could have been another amount…
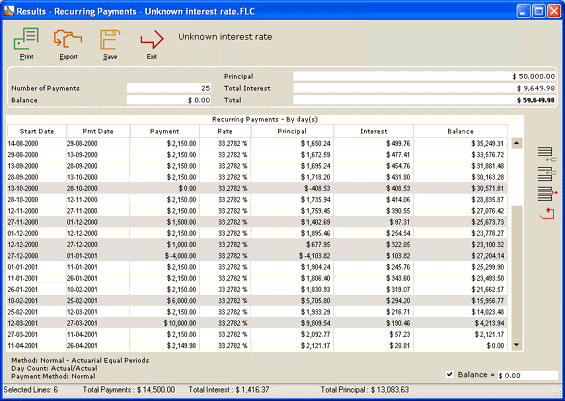
Simply highlight all the lines (rates) to be recalculated or some of the lines (only the interest rates in these lines will be recalculated) and right click:

APR (Annual Percentage Rate) calculation
Margill easily calculates APR for regular and irregular loans and mortgages at fixed or variable interest rates. This is done in the “Recurring payments (Amortization)” calculation.
As can be seen in the screen shot below, the fees may be financed or paid up front. Depending on each case, the APR will vary slightly.

Margill includes APR (nominal APR as used in certain laws such as the US Truth in Lending Act) and the Effective APR that factors in the compounding period as required notably in European countries.
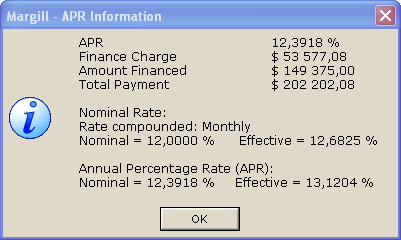
Lending laws usually allow between 1/8% to 1/4% tolerance (maximum discrepancy) between quoted APR and the true APR (based on the various legislative formulae).
Complex APR calculation
The APR can also be calculated for more complex loans that involve irregular payments, variable interest rates, additional principal, etc. As can be seen in the example below, Margill is very powerful for APR calculations.
This loan (only part of the loan is seen below) includes irregular payment dates, irregular payment amounts, a missed payment (0.00), additional principal (-25,000), lump sums (5000 and 10,000) and an interest rate that changes on July 1 (date format is DD/MMD/YYYY in this example but could be any other format).
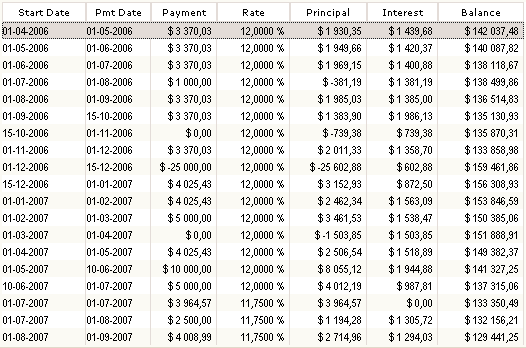
The final lines of the loan appear below. In order to calculate APR, the formula requires that the balance = 0.00 (this way all finance charges are known).

The APR report can then be printed or saved:

